Using a compass to calculate distance

Sometimes while hiking you need to know the distance of something. Like a mountain, a river width or a distant hut.
To do this you will need a compass.
For this example, We'll work out how far away a hut is to see how long it will take to walk there.
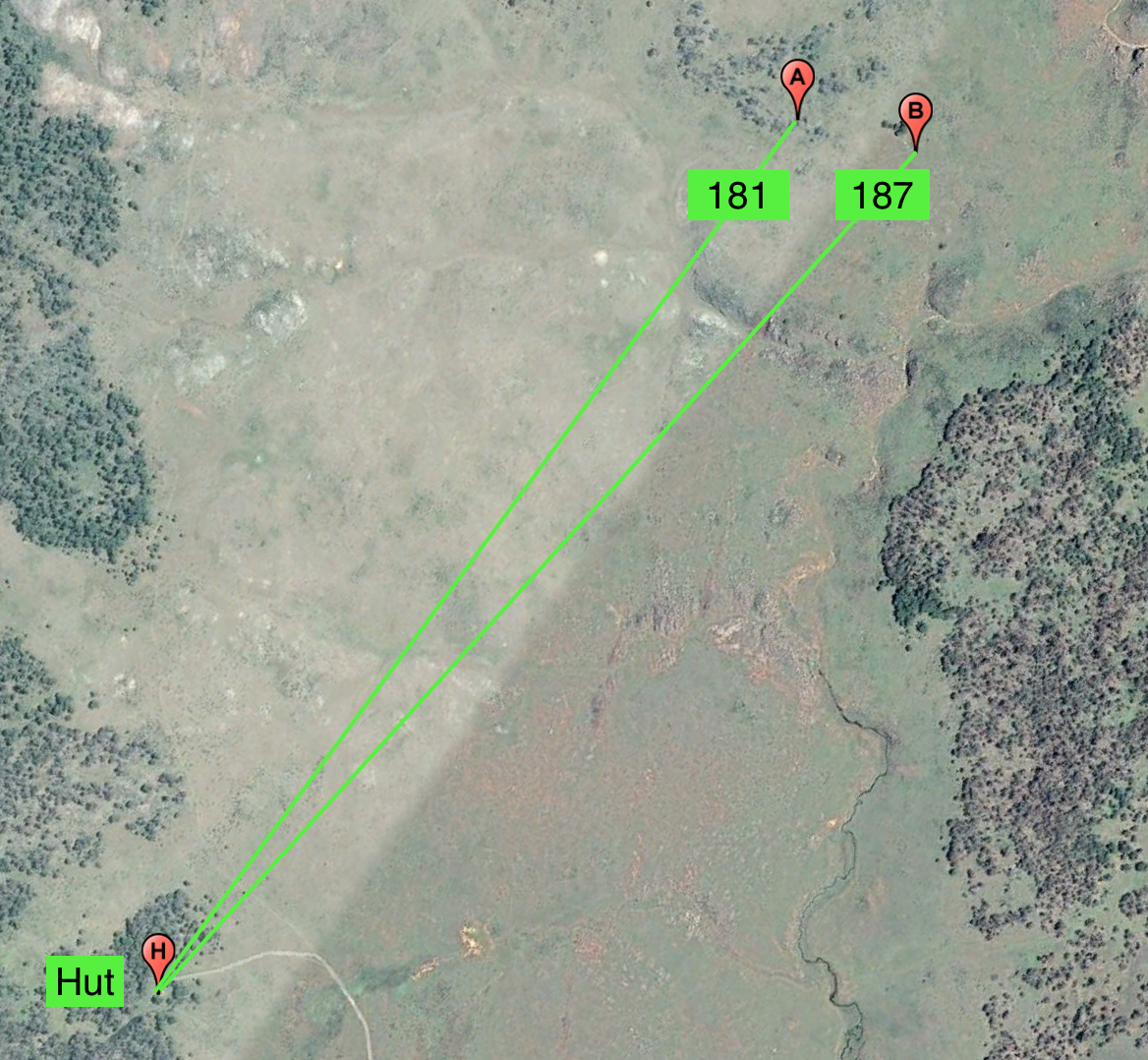
- Firstly, We take a compass bearing of the hut. It's 181 degrees. This bearing will be A. A = 181
- Now, we need to walk 200m perpendicular to the hut to take a second bearing. The reference distance we walked will be Ref. Ref = 200
(This can be any distance, 10m or 1km) - Now we take a second bearing. It's 187 degrees. This bearing will be B. B = 187
We now have all the values we need to calculate the distance to the hut with this simple formula:
Distance = (Tan (90 - (A -B))) x Ref
We can work out the formula in on the trail in 4 simple steps.
A - B = C
90 - C = D
Tan(D) = T
T x Ref = Distance to hut
So with our first bearing, we subtract the smaller value from the other. In this case it's B.
187 - 181 = 6
We then subtract the answer from 90.
90 - 6 = 84
We then get the TAN of that answer
Tan(84) = 9.51
We then use that answer and multiple it by the reference distance R.
9.51 x 200 = 1903
The result is the distance in meters. 1,903m or 1.9km.
An easy way to get the reference distance between your two bearings is it waypoint your first bearing in your GPS and get the distance to Waypoint at your second bearing. This is handy when your reference distance is 1km or more.
You can also print out a table below with calculated Tan values. This way you don't need a calculator on the trail.
| 1 | 0.017 |
| 2 | 0.035 |
| 3 | 0.052 |
| 4 | 0.070 |
| 5 | 0.087 |
| 6 | 0.105 |
| 7 | 0.123 |
| 8 | 0.141 |
| 9 | 0.158 |
| 10 | 0.176 |
| 11 | 0.194 |
| 12 | 0.213 |
| 13 | 0.231 |
| 14 | 0.249 |
| 15 | 0.268 |
| 16 | 0.287 |
| 17 | 0.306 |
| 18 | 0.325 |
| 19 | 0.344 |
| 20 | 0.364 |
| 21 | 0.384 |
| 22 | 0.404 |
| 23 | 0.424 |
| 24 | 0.445 |
| 25 | 0.466 |
| 26 | 0.488 |
| 27 | 0.510 |
| 28 | 0.532 |
| 29 | 0.554 |
| 30 | 0.577 |
| 31 | 0.601 |
| 32 | 0.625 |
| 33 | 0.649 |
| 34 | 0.675 |
| 35 | 0.700 |
| 36 | 0.727 |
| 37 | 0.754 |
| 38 | 0.781 |
| 39 | 0.810 |
| 40 | 0.839 |
| 41 | 0.869 |
| 42 | 0.900 |
| 43 | 0.933 |
| 44 | 0.966 |
| 45 | 1.000 |
| 46 | 1.036 |
| 47 | 1.072 |
| 48 | 1.111 |
| 49 | 1.150 |
| 50 | 1.192 |
| 51 | 1.235 |
| 52 | 1.280 |
| 53 | 1.327 |
| 54 | 1.376 |
| 55 | 1.428 |
| 56 | 1.483 |
| 57 | 1.540 |
| 58 | 1.600 |
| 59 | 1.664 |
| 60 | 1.732 |
| 61 | 1.804 |
| 62 | 1.881 |
| 63 | 1.963 |
| 64 | 2.050 |
| 65 | 2.145 |
| 66 | 2.246 |
| 67 | 2.356 |
| 68 | 2.475 |
| 69 | 2.605 |
| 70 | 2.747 |
| 71 | 2.904 |
| 72 | 3.078 |
| 73 | 3.271 |
| 74 | 3.487 |
| 75 | 3.732 |
| 76 | 4.011 |
| 77 | 4.331 |
| 78 | 4.705 |
| 79 | 5.145 |
| 80 | 5.671 |
| 81 | 6.314 |
| 82 | 7.115 |
| 83 | 8.144 |
| 84 | 9.514 |
| 85 | 11.430 |
| 86 | 14.301 |
| 87 | 19.081 |
| 88 | 28.636 |
| 89 | 57.290 |